Concave Mirrors for Herriott Cells (2 - 20 µm)

- Mid-Infrared Enhanced Gold Mirrors for Herriott Cells
- Concave Mirrors with or without Through Hole
- 1" or 2" Outer Diameter
CM508-200EH4-M02
Ø2" Concave Mirror with
Ø4 mm Off-Axis Hole
CM254-100-M02
Ø1" Concave Mirror
CM254-100CH3-M02
Ø1" Concave Mirror with
Ø3 mm Center Hole
A Herriott Cell Increases the Path Length
of a Beam Through the Cell

Please Wait
Click to Enlarge
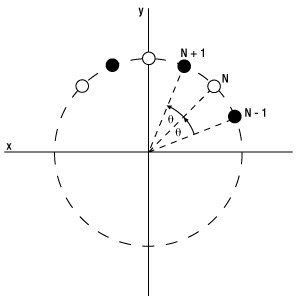
The figure above shows the angle θ as seen projected upon the mirror's surface. The solid circles represent reflections on one mirror and the open circles represent reflections on the other mirror.

Click to Enlarge
Thorlabs also offers complete Herriott cells that incorporate our Ø2" concave mirrors with off-set holes.
Features
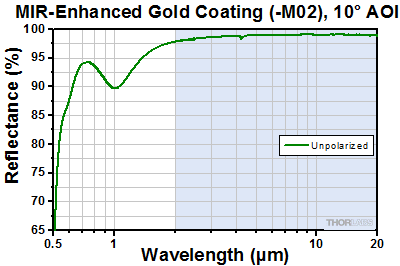
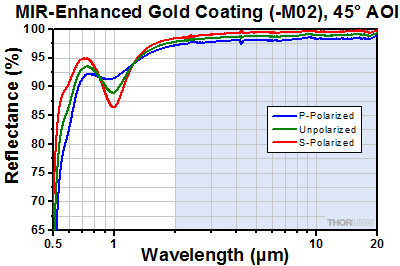
- Mid-Infrared Enhanced Gold Herriott Cell Mirrors: 2 - 20 µm, Ravg > 98% and Rabs > 95%
- Ø1" Mirrors with f = 100.0 mm and Ø2" Mirrors with f = 200.0 mm
- Available with or without Through Hole
- Through Hole Available as Center or Off-Axis Hole
- UVFS Substrate for Improved Thermal Stability
Thorlabs' Concave Mirrors for Herriott Cells are designed for the construction of table-top Herriott cells. Both Ø1" (f = 100 mm) and Ø2" (f = 200 mm) mirrors are available, either with or without a through hole. Due to the overcoat on these mirrors, they are more resilient to humidity, moisture absorption, and other environmental effects than our standard gold-coated concave mirrors. This overcoat also provides enhanced performance in the mid-infrared (MIR), with a >98% average reflectance between 2 μm to 20 μm. Since Herriott cells involve multiple reflections, they are sensitive to small thermal shifts, which can impact the output alignment. These mirrors are made with UFVS substrates to provide improved thermal stability and help maintain output optical alignment.
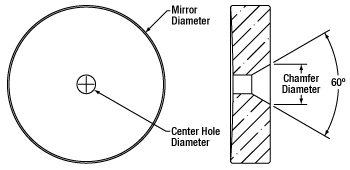
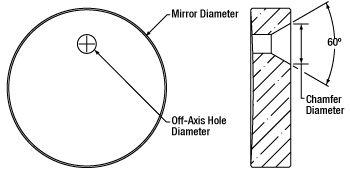
A Herriott cell is created using two spherical mirrors (with the same focal length) to construct a cavity, with at least one of the mirrors containing a hole (either centered or off-axis). Light is injected and ejected through the hole in the mirror and makes multiple bounces within the cell before returning to its entrance point (see image above). To aid in injecting light into a Herriott cell, our mirrors with through holes have large hole diameters on the back side (Ø6.5 to Ø6.6 mm for our Ø1" mirrors and Ø8.0 mm for our Ø2" mirrors) with a 60° chamfer. Thorlabs also offers complete, pre-aligned Herriott cells that incorporate our Ø2" concave mirrors with off-axis holes (Item # CM508-200EH4-M02).
Herriott cells are a form of long-optical-path absorption cells and are used primarily for weak-trace-gas absorption spectroscopy applications such as environmental monitoring, combustion processes, medical diagnostics, and fundamental atomic and molecular physics. Compared to other long-optical-path absorption cells, such as the White cell, the Herriott cell is more stable to small perturbations. The major advantages of the Herriott cell are that it provides a relatively long absorption path in a compact design and that it is much simpler than high-finesse optical cavities (which would typically require spatial mode matching, precise optical alignment, or resonant excitation)a,b,c. For example, using our Ø2" center hole mirror with a cavity length of 363 mm and a Ø2 mm beam, a path length of 12.5 m can be realized. Similarly, using our Ø2" off-axis hole mirror with a cavity length of 374 mm and a Ø1 mm beam, a path length of 35.9 m can be realized. The beam path length can be approximated by multiplying the distance between the mirrors by the number of spots (i.e., reflections) on each mirror.a Longer path lengths can be achieved by increasing the number of spots on each mirror.
When a beam is injected into a Herriott cell, it is reflected multiple times between the two mirrors, always staying on the surface of a rotational hyperboloid. When viewed on the surface of the mirror, the reflection points of the beam lie, in general, on an ellipse or circle (see figure to the right). In the special case of the mirror with a center hole, the reflection points lie upon a line (though it is still possible to generate an ellipse under certain geometries). This means that, generally, the off-axis hole mirrors can produce longer path lengths than the center hole mirrors, since the off-axis hole mirrors can use more of the mirror's aperture. The angle θ is the angle (in radians) between two successive reflections (hence the reflection points are rotated by 2θ on any one given mirror). Thus the re-entrant condition (the condition under which the beam will retrace its path) for a Herriott cell is given by:
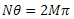
Where N (an even integer) is the total number of passes the beam makes within the cell and M is an integer. For mirrors with a center hole, θ is equal to pi. The equation above simply states that the number of total reflections multiplied by the angle between successive reflections must be an integer multiple of 2pi in order to exit the Herriott cell. The number of reflections the beam takes within the cell is controlled by adjusting the distance between the two mirrors. Due to the simplicity and stability of the device, the Herriott cell provides a convenient tool to increase the optical path length of a beam while keeping the device compact and manageable.
The shaded region in the graphs below denotes the range over which we guarantee the specified reflectance. Please note that the reflectance outside of this band is typical and can vary from lot to lot, especially in out-of-band regions where the reflectance is fluctuating or sloped.
| Damage Threshold Specifications | ||
|---|---|---|
| Coating Designation (Item # Suffix) |
Damage Threshold | |
| -M02 | Pulsed | 0.1 J/cm2 at 1.064 µm, 10 ns, 10 Hz, Ø1.06 mm 3 J/cm2 at 10.6 µm, 100 ns, 1 Hz, Ø1.29 mm |
| CWa | 25 W/cm at 1.07 µm, Ø1.04 mm 450 W/cm at 10.6 µm, Ø1.18 mm |
|
Damage Threshold Data for Thorlabs' Mid-Infrared Enhanced Mirrors
The specifications to the right are measured data for Thorlabs' mid-infrared enhanced gold mirror coatings. Damage threshold specifications are constant for a given coating type, regardless of the size or shape of the mirror.
Laser Induced Damage Threshold Tutorial
The following is a general overview of how laser induced damage thresholds are measured and how the values may be utilized in determining the appropriateness of an optic for a given application. When choosing optics, it is important to understand the Laser Induced Damage Threshold (LIDT) of the optics being used. The LIDT for an optic greatly depends on the type of laser you are using. Continuous wave (CW) lasers typically cause damage from thermal effects (absorption either in the coating or in the substrate). Pulsed lasers, on the other hand, often strip electrons from the lattice structure of an optic before causing thermal damage. Note that the guideline presented here assumes room temperature operation and optics in new condition (i.e., within scratch-dig spec, surface free of contamination, etc.). Because dust or other particles on the surface of an optic can cause damage at lower thresholds, we recommend keeping surfaces clean and free of debris. For more information on cleaning optics, please see our Optics Cleaning tutorial.
Testing Method
Thorlabs' LIDT testing is done in compliance with ISO/DIS 11254 and ISO 21254 specifications.
First, a low-power/energy beam is directed to the optic under test. The optic is exposed in 10 locations to this laser beam for 30 seconds (CW) or for a number of pulses (pulse repetition frequency specified). After exposure, the optic is examined by a microscope (~100X magnification) for any visible damage. The number of locations that are damaged at a particular power/energy level is recorded. Next, the power/energy is either increased or decreased and the optic is exposed at 10 new locations. This process is repeated until damage is observed. The damage threshold is then assigned to be the highest power/energy that the optic can withstand without causing damage. A histogram such as that below represents the testing of one BB1-E02 mirror.

The photograph above is a protected aluminum-coated mirror after LIDT testing. In this particular test, it handled 0.43 J/cm2 (1064 nm, 10 ns pulse, 10 Hz, Ø1.000 mm) before damage.
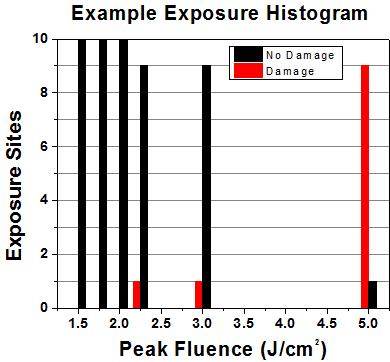
| Example Test Data | |||
|---|---|---|---|
| Fluence | # of Tested Locations | Locations with Damage | Locations Without Damage |
| 1.50 J/cm2 | 10 | 0 | 10 |
| 1.75 J/cm2 | 10 | 0 | 10 |
| 2.00 J/cm2 | 10 | 0 | 10 |
| 2.25 J/cm2 | 10 | 1 | 9 |
| 3.00 J/cm2 | 10 | 1 | 9 |
| 5.00 J/cm2 | 10 | 9 | 1 |
According to the test, the damage threshold of the mirror was 2.00 J/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.803 mm). Please keep in mind that these tests are performed on clean optics, as dirt and contamination can significantly lower the damage threshold of a component. While the test results are only representative of one coating run, Thorlabs specifies damage threshold values that account for coating variances.
Continuous Wave and Long-Pulse Lasers
When an optic is damaged by a continuous wave (CW) laser, it is usually due to the melting of the surface as a result of absorbing the laser's energy or damage to the optical coating (antireflection) [1]. Pulsed lasers with pulse lengths longer than 1 µs can be treated as CW lasers for LIDT discussions.
When pulse lengths are between 1 ns and 1 µs, laser-induced damage can occur either because of absorption or a dielectric breakdown (therefore, a user must check both CW and pulsed LIDT). Absorption is either due to an intrinsic property of the optic or due to surface irregularities; thus LIDT values are only valid for optics meeting or exceeding the surface quality specifications given by a manufacturer. While many optics can handle high power CW lasers, cemented (e.g., achromatic doublets) or highly absorptive (e.g., ND filters) optics tend to have lower CW damage thresholds. These lower thresholds are due to absorption or scattering in the cement or metal coating.

LIDT in linear power density vs. pulse length and spot size. For long pulses to CW, linear power density becomes a constant with spot size. This graph was obtained from [1].
Pulsed lasers with high pulse repetition frequencies (PRF) may behave similarly to CW beams. Unfortunately, this is highly dependent on factors such as absorption and thermal diffusivity, so there is no reliable method for determining when a high PRF laser will damage an optic due to thermal effects. For beams with a high PRF both the average and peak powers must be compared to the equivalent CW power. Additionally, for highly transparent materials, there is little to no drop in the LIDT with increasing PRF.
In order to use the specified CW damage threshold of an optic, it is necessary to know the following:
- Wavelength of your laser
- Beam diameter of your beam (1/e2)
- Approximate intensity profile of your beam (e.g., Gaussian)
- Linear power density of your beam (total power divided by 1/e2 beam diameter)
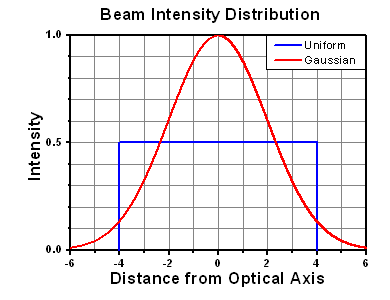
Thorlabs expresses LIDT for CW lasers as a linear power density measured in W/cm. In this regime, the LIDT given as a linear power density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size, as demonstrated by the graph to the right. Average linear power density can be calculated using the equation below.
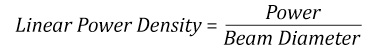
The calculation above assumes a uniform beam intensity profile. You must now consider hotspots in the beam or other non-uniform intensity profiles and roughly calculate a maximum power density. For reference, a Gaussian beam typically has a maximum power density that is twice that of the uniform beam (see lower right).
Now compare the maximum power density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately. A good rule of thumb is that the damage threshold has a linear relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 10 W/cm at 1310 nm scales to 5 W/cm at 655 nm):

While this rule of thumb provides a general trend, it is not a quantitative analysis of LIDT vs wavelength. In CW applications, for instance, damage scales more strongly with absorption in the coating and substrate, which does not necessarily scale well with wavelength. While the above procedure provides a good rule of thumb for LIDT values, please contact Tech Support if your wavelength is different from the specified LIDT wavelength. If your power density is less than the adjusted LIDT of the optic, then the optic should work for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. The damage analysis will be carried out on a similar optic (customer's optic will not be damaged). Testing may result in additional costs or lead times. Contact Tech Support for more information.
Pulsed Lasers
As previously stated, pulsed lasers typically induce a different type of damage to the optic than CW lasers. Pulsed lasers often do not heat the optic enough to damage it; instead, pulsed lasers produce strong electric fields capable of inducing dielectric breakdown in the material. Unfortunately, it can be very difficult to compare the LIDT specification of an optic to your laser. There are multiple regimes in which a pulsed laser can damage an optic and this is based on the laser's pulse length. The highlighted columns in the table below outline the relevant pulse lengths for our specified LIDT values.
Pulses shorter than 10-9 s cannot be compared to our specified LIDT values with much reliability. In this ultra-short-pulse regime various mechanics, such as multiphoton-avalanche ionization, take over as the predominate damage mechanism [2]. In contrast, pulses between 10-7 s and 10-4 s may cause damage to an optic either because of dielectric breakdown or thermal effects. This means that both CW and pulsed damage thresholds must be compared to the laser beam to determine whether the optic is suitable for your application.
| Pulse Duration | t < 10-9 s | 10-9 < t < 10-7 s | 10-7 < t < 10-4 s | t > 10-4 s |
|---|---|---|---|---|
| Damage Mechanism | Avalanche Ionization | Dielectric Breakdown | Dielectric Breakdown or Thermal | Thermal |
| Relevant Damage Specification | No Comparison (See Above) | Pulsed | Pulsed and CW | CW |
When comparing an LIDT specified for a pulsed laser to your laser, it is essential to know the following:
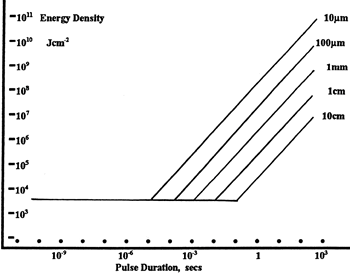
LIDT in energy density vs. pulse length and spot size. For short pulses, energy density becomes a constant with spot size. This graph was obtained from [1].
- Wavelength of your laser
- Energy density of your beam (total energy divided by 1/e2 area)
- Pulse length of your laser
- Pulse repetition frequency (prf) of your laser
- Beam diameter of your laser (1/e2 )
- Approximate intensity profile of your beam (e.g., Gaussian)
The energy density of your beam should be calculated in terms of J/cm2. The graph to the right shows why expressing the LIDT as an energy density provides the best metric for short pulse sources. In this regime, the LIDT given as an energy density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size. This calculation assumes a uniform beam intensity profile. You must now adjust this energy density to account for hotspots or other nonuniform intensity profiles and roughly calculate a maximum energy density. For reference a Gaussian beam typically has a maximum energy density that is twice that of the 1/e2 beam.
Now compare the maximum energy density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately [3]. A good rule of thumb is that the damage threshold has an inverse square root relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 1 J/cm2 at 1064 nm scales to 0.7 J/cm2 at 532 nm):
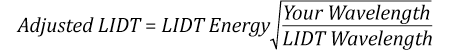
You now have a wavelength-adjusted energy density, which you will use in the following step.
Beam diameter is also important to know when comparing damage thresholds. While the LIDT, when expressed in units of J/cm², scales independently of spot size; large beam sizes are more likely to illuminate a larger number of defects which can lead to greater variances in the LIDT [4]. For data presented here, a <1 mm beam size was used to measure the LIDT. For beams sizes greater than 5 mm, the LIDT (J/cm2) will not scale independently of beam diameter due to the larger size beam exposing more defects.
The pulse length must now be compensated for. The longer the pulse duration, the more energy the optic can handle. For pulse widths between 1 - 100 ns, an approximation is as follows:
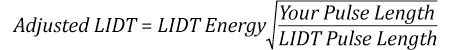
Use this formula to calculate the Adjusted LIDT for an optic based on your pulse length. If your maximum energy density is less than this adjusted LIDT maximum energy density, then the optic should be suitable for your application. Keep in mind that this calculation is only used for pulses between 10-9 s and 10-7 s. For pulses between 10-7 s and 10-4 s, the CW LIDT must also be checked before deeming the optic appropriate for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. Contact Tech Support for more information.
[1] R. M. Wood, Optics and Laser Tech. 29, 517 (1998).
[2] Roger M. Wood, Laser-Induced Damage of Optical Materials (Institute of Physics Publishing, Philadelphia, PA, 2003).
[3] C. W. Carr et al., Phys. Rev. Lett. 91, 127402 (2003).
[4] N. Bloembergen, Appl. Opt. 12, 661 (1973).
In order to illustrate the process of determining whether a given laser system will damage an optic, a number of example calculations of laser induced damage threshold are given below. For assistance with performing similar calculations, we provide a spreadsheet calculator that can be downloaded by clicking the button to the right. To use the calculator, enter the specified LIDT value of the optic under consideration and the relevant parameters of your laser system in the green boxes. The spreadsheet will then calculate a linear power density for CW and pulsed systems, as well as an energy density value for pulsed systems. These values are used to calculate adjusted, scaled LIDT values for the optics based on accepted scaling laws. This calculator assumes a Gaussian beam profile, so a correction factor must be introduced for other beam shapes (uniform, etc.). The LIDT scaling laws are determined from empirical relationships; their accuracy is not guaranteed. Remember that absorption by optics or coatings can significantly reduce LIDT in some spectral regions. These LIDT values are not valid for ultrashort pulses less than one nanosecond in duration.

A Gaussian beam profile has about twice the maximum intensity of a uniform beam profile.
CW Laser Example
Suppose that a CW laser system at 1319 nm produces a 0.5 W Gaussian beam that has a 1/e2 diameter of 10 mm. A naive calculation of the average linear power density of this beam would yield a value of 0.5 W/cm, given by the total power divided by the beam diameter:
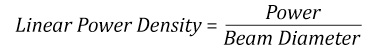
However, the maximum power density of a Gaussian beam is about twice the maximum power density of a uniform beam, as shown in the graph to the right. Therefore, a more accurate determination of the maximum linear power density of the system is 1 W/cm.
An AC127-030-C achromatic doublet lens has a specified CW LIDT of 350 W/cm, as tested at 1550 nm. CW damage threshold values typically scale directly with the wavelength of the laser source, so this yields an adjusted LIDT value:

The adjusted LIDT value of 350 W/cm x (1319 nm / 1550 nm) = 298 W/cm is significantly higher than the calculated maximum linear power density of the laser system, so it would be safe to use this doublet lens for this application.
Pulsed Nanosecond Laser Example: Scaling for Different Pulse Durations
Suppose that a pulsed Nd:YAG laser system is frequency tripled to produce a 10 Hz output, consisting of 2 ns output pulses at 355 nm, each with 1 J of energy, in a Gaussian beam with a 1.9 cm beam diameter (1/e2). The average energy density of each pulse is found by dividing the pulse energy by the beam area:
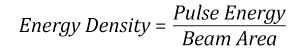
As described above, the maximum energy density of a Gaussian beam is about twice the average energy density. So, the maximum energy density of this beam is ~0.7 J/cm2.
The energy density of the beam can be compared to the LIDT values of 1 J/cm2 and 3.5 J/cm2 for a BB1-E01 broadband dielectric mirror and an NB1-K08 Nd:YAG laser line mirror, respectively. Both of these LIDT values, while measured at 355 nm, were determined with a 10 ns pulsed laser at 10 Hz. Therefore, an adjustment must be applied for the shorter pulse duration of the system under consideration. As described on the previous tab, LIDT values in the nanosecond pulse regime scale with the square root of the laser pulse duration:
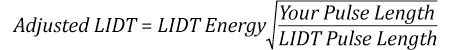
This adjustment factor results in LIDT values of 0.45 J/cm2 for the BB1-E01 broadband mirror and 1.6 J/cm2 for the Nd:YAG laser line mirror, which are to be compared with the 0.7 J/cm2 maximum energy density of the beam. While the broadband mirror would likely be damaged by the laser, the more specialized laser line mirror is appropriate for use with this system.
Pulsed Nanosecond Laser Example: Scaling for Different Wavelengths
Suppose that a pulsed laser system emits 10 ns pulses at 2.5 Hz, each with 100 mJ of energy at 1064 nm in a 16 mm diameter beam (1/e2) that must be attenuated with a neutral density filter. For a Gaussian output, these specifications result in a maximum energy density of 0.1 J/cm2. The damage threshold of an NDUV10A Ø25 mm, OD 1.0, reflective neutral density filter is 0.05 J/cm2 for 10 ns pulses at 355 nm, while the damage threshold of the similar NE10A absorptive filter is 10 J/cm2 for 10 ns pulses at 532 nm. As described on the previous tab, the LIDT value of an optic scales with the square root of the wavelength in the nanosecond pulse regime:
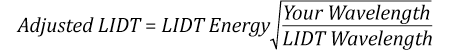
This scaling gives adjusted LIDT values of 0.08 J/cm2 for the reflective filter and 14 J/cm2 for the absorptive filter. In this case, the absorptive filter is the best choice in order to avoid optical damage.
Pulsed Microsecond Laser Example
Consider a laser system that produces 1 µs pulses, each containing 150 µJ of energy at a repetition rate of 50 kHz, resulting in a relatively high duty cycle of 5%. This system falls somewhere between the regimes of CW and pulsed laser induced damage, and could potentially damage an optic by mechanisms associated with either regime. As a result, both CW and pulsed LIDT values must be compared to the properties of the laser system to ensure safe operation.
If this relatively long-pulse laser emits a Gaussian 12.7 mm diameter beam (1/e2) at 980 nm, then the resulting output has a linear power density of 5.9 W/cm and an energy density of 1.2 x 10-4 J/cm2 per pulse. This can be compared to the LIDT values for a WPQ10E-980 polymer zero-order quarter-wave plate, which are 5 W/cm for CW radiation at 810 nm and 5 J/cm2 for a 10 ns pulse at 810 nm. As before, the CW LIDT of the optic scales linearly with the laser wavelength, resulting in an adjusted CW value of 6 W/cm at 980 nm. On the other hand, the pulsed LIDT scales with the square root of the laser wavelength and the square root of the pulse duration, resulting in an adjusted value of 55 J/cm2 for a 1 µs pulse at 980 nm. The pulsed LIDT of the optic is significantly greater than the energy density of the laser pulse, so individual pulses will not damage the wave plate. However, the large average linear power density of the laser system may cause thermal damage to the optic, much like a high-power CW beam.
Insights into Mirrors for Herriott Cells
Scroll down to read about:
- Setting up and Aligning a Herriott Cell
Click here for more insights into lab practices and equipment.
Herriott Cell Setup and Configuration (Viewer Inspired)
In a Herriott cell, light reflects multiple times between two concave mirrors. The reflected beams cross the volume between the two mirrors at different angles, tracing out different paths and creating linear, elliptical, or circular spot patterns on the mirrors. To allow the beam to enter and exit the cell, one or both of the mirrors typically has a hole at its center or near its edge. Herriott cells are used in a variety of applications that benefit from folding a long optical path length into a compact space. Gas-absorption spectroscopy is a popular application, since every additional pass of the beam through the sample volume increases the signal-to-noise ratio of the measurement data.
This demonstration begins with a roughly aligned setup, in which one mirror has a hole near its edge and the other has no hole. Both mirrors have the same focal length. A non-polarizing beamsplitter and a pair of irises are used to set the mirror orientations so they are parallel to each other and perpendicular to a line of screw holes in the table. After this procedure is completed, the angular orientations of the mirrors are no longer adjusted. The demonstration then shows how to achieve different reflection patterns on the mirrors by changing the input beam orientation and cell length.
Both the input beam angle and mirror spacing affect the number of reflections the beam experiences before exiting the cell. A special case is when the two mirrors have the same focal length and are separated by a distance equal to the focal length. This configuration always provides six passes through the cell, regardless of the orientation of the input beam. This mirror spacing is used to illustrate the effects of changing the input beam’s pitch and yaw angles, as well as the beam’s X-axis and Y-axis position. In addition, the input beam is aligned parallel to the cell’s optical axis as a starting point. Then, the cell length is adjusted to increase the number of passes through the cell. Further adjustments to the input beam orientation are demonstrated to create linear, elliptical, and circular reflection patterns.
If you would like more information about tips, tricks, and other methods we often use in the lab, we recommend our other Video Insights. In addition, our webinars provide practical and theoretical introductions to our different products.
References:
D. Herriott et al., Appl. Opt. 3, 523-526 (1964).
C.G.Tarsitano et al., Appl. Opt. 46, 6923-6935 (2007).
| Products Featured During Demonstration | |||
| Gold-Coated Herriott Cell Mirrors | 637 nm Benchtop Laser Source | Non-Polarizing Beamsplitter | Kinematic Mount |
| Mirror Mount | Six-Axis Kinematic Mount | Irises | Single Mode Fiber Patch Cable |
| Linear Translation Stage | Fiber Collimator and Threaded Mount Adapter |
Iris Mount | Post Collars |
| Quick-Connect Stage Platform | Flexure Clamping Base | Magnetic Pedestal Base | Magnetic Ruler |
Date of Last Edit: Jul. 14, 2023
| Posted Comments: | |
Jaskaran Singh
(posted 2020-02-20 06:54:44.38) I have a query related number of spots calculation with your products CM254-100EH3-M02 (off-axis hole) and CM254-100-M02 (no hole). Please help me with this query. Thank You. nbayconich
(posted 2020-02-24 08:31:41.0) Thank you for contacting Thorlabs. I will reach out to you directly to discuss your application, for reference the number spots or passes in your system can be controlled by adjusting the distance between two mirrors, the number of passes in the cell can be related by the equation NΘ = 2*M*π. user
(posted 2019-08-06 08:47:47.083) Dear Sir
Is there any possibility to pourchase these mirrors with radius of curvature of 1 m ?
regards, T. Stacewicz
prof. dr hab. Tadeusz Stacewicz
University of Warsaw
Faculty of Physics
Institute of Experimental Physics
Optics Division
Pasteura 5, 02-093 Warsaw, Poland
tel. +48 22 55 32 734 user
(posted 2019-08-06 08:46:28.883) Dear Sir
Is there any possibility to pourchase these mirrors with radius of curvature of 1 m ?
regards, T. Stacewicz
prof. dr hab. Tadeusz Stacewicz
University of Warsaw
Faculty of Physics
Institute of Experimental Physics
Optics Division
Pasteura 5, 02-093 Warsaw, Poland
tel. +48 22 55 32 734 YLohia
(posted 2019-08-06 04:02:18.0) Hello Tadeusz, thank you for contacting Thorlabs. For custom item requests, please email your local Thorlabs Tech Support team (techsupport.se@thorlabs.com in your case). We will reach out to you directly. miroslav.kloz
(posted 2018-09-03 15:27:56.403) Dear Mr/Ms,
Is it possible to obtain 1" spherical mirrors with a 3 mm hole in the center also in different coatings, possibly a different focal lengths?
More specifically:
1", UV enhanced aluminum, 200 or 500 mm focal length?
We would definitely buy more than one if these are available.
M.Kloz nbayconich
(posted 2018-09-05 10:04:41.0) Thank you for contacting Thorlabs. Yes we can provide custom made mirrors such as these upon request. I will reach out to you directly with more information about our custom capabilities.
For any custom requests please contact us directly at techsupport@thorlabs.com. user
(posted 2018-01-22 16:19:57.09) What is the tolerance on the focal length or radius of curvature of the f = 200 mm mirrors? (f = 200 mm +- ? mm)
Thanks! nbayconich
(posted 2018-03-30 04:44:53.0) Thank you for contacting Thorlabs. We do not specify a focal length tolerance but the typical focal length tolerance will be ±1% of the focal length. abekal
(posted 2017-05-30 16:49:55.397) Can you provide holes in the multipass mirrors at custom location? nbayconich
(posted 2017-06-13 02:48:00.0) Thank you for contacting Thorlabs. Yes we can offer custom hole locations. I will reach out to you directly about our custom capabilities. hossein.aghai-khozani
(posted 2014-12-03 12:07:18.377) Hi,
is it possible to get these Herriot cell mirrors with protected silver coatings and 500m focal length?
cheers cdaly
(posted 2014-12-04 02:37:55.0) Response from Chris at Thorlabs: Yes, we can put our other coatings on the mirrors and provide custom focal lengths for sufficient quantities. We will contact you directly about this, but we can be reached at techsupport@thorlabs.com for future custom inquiries. |

| Item # | CM254-100-M02 | CM508-200-M02 |
|---|---|---|
| Outer Diameter | 1" | 2" |
| Focal Length | 100.0 mm | 200.0 mm |
| Clear Aperture | >Ø22.86 mm | >Ø45.72 mm |
| Reflectance | Ravg > 98%, Rabs > 95% from 2.0 - 20.0 µm |
|
| Reflectance Curve (Click for Plot) |
Click Here for Raw Data
|
|
| Surface Quality | 40-20 Scratch-Dig Over Clear Aperture | |
| Power Tolerance | <λ/2 @ 633 nm Over Clear Aperture | |
| Surface Irregularity | <λ/4 @ 633 nm Over Clear Aperture | |
| Back Surface Finish | Uniform Fine Grind #12-20 Grit | |
| Coating | Gold with Protective Overcoat Per MIL-C-48497A | |
| Substrate | UV Fused Silicaa | |

| Item # | CM254-100CH3-M02 | CM508-200CH4-M02 |
|---|---|---|
| Outer Diameter | 1" | 2" |
| Focal Length | 100.0 mm | 200.0 mm |
| Clear Aperture | >Ø22.86 mm | >Ø45.72 mm |
| Center Hole | Ø3.0 mm | Ø4.0 mm |
| Reflectance | Ravg > 98%, Rabs > 95% from 2.0 - 20.0 µm |
|
| Reflectance Curve (Click for Plot) |
Click Here for Raw Data
|
|
| Surface Quality | 40-20 Scratch-Dig Over Clear Aperture | |
| Power Tolerance | <λ/2 @ 633 nm Over Clear Aperture | |
| Surface Irregularity | <λ/4 @ 633 nm Over Clear Aperture | |
| Back Surface Finish | Uniform Fine Grind #12-20 Grit | |
| Coating | Gold with Protective Overcoat Per MIL-C-48497A | |
| Substrate | UV Fused Silicaa | |

| Item # | CM254-100EH3-M02 | CM508-200EH4-M02 |
|---|---|---|
| Outer Diameter | 1" | 2" |
| Focal Length | 100.0 mm | 200.0 mm |
| Clear Aperture | >Ø22.86 mm | >Ø45.72 mm |
| Off-Axis Hole | Ø3.0 mm (7.0 mm from Center) |
Ø4.0 mm (20.0 mm from Center) |
| Reflectance | Ravg > 98%, Rabs > 95% from 2.0 - 20.0 µm |
|
| Reflectance Curve (Click for Plot) |
Click Here for Raw Data
|
|
| Surface Quality | 40-20 Scratch-Dig Over Clear Aperture | |
| Power Tolerance | <λ/2 @ 633 nm Over Clear Aperture | |
| Surface Irregularity | <λ/4 @ 633 nm Over Clear Aperture | |
| Back Surface Finish | Uniform Fine Grind #12-20 Grit | |
| Coating | Gold with Protective Overcoat Per MIL-C-48497A | |
| Substrate | UV Fused Silicaa | |
 Products Home
Products Home


















 Zoom
Zoom


 Gold-Coated Herriott Cell Mirrors
Gold-Coated Herriott Cell Mirrors